Алгоритм пчел для оптимизации функции
Оглавление
Введение
Основные принципы
Реализация алгоритма на Python
Пример работы алгоритма
Заключение
Ссылки
Комментарии
Введение
Алгоритм пчел (в англоязычных статьях так же встречаются названия Artificial Bee Colony Algorithm и Bees Algorithm) является довольно молодым алгоритмом для нахождения глобальных экстремумов (максимумов или минимумов) сложных многомерных функций (будем называть эту функцию целевой функцией). Первые статьи, которые удалось найти в интернете, датируются 2005 годом ([1] и [2]). Кроме того, например, в [3] тоже довольно хорошо описана суть этого алгоритма, приведено сравнение алгоритма пчел с генетическим алгоритмом и алгоритмом, моделирующим поведение муравьев. Там же, в [3], можно найти несколько интересных функций, на которых можно отрабатывать алгоритм.
В этой статье мы рассмотрим основные принципы алгоритма и пример его реализации на языке Python.
Основные принципы
Идея алгоритма взята, как уже можно догадаться из названия, у пчел, а именно из их поведения при поиске мест, где можно раздобыть как можно больше нектара. Сначала из улея вылетают в случайно направлении какое-то количество пчел-разведчиков, которые пытаются отыскать участки, где есть нектар. Через какое-то время пчелы возвращаются в улей и особым образом сообщают остальным где и сколько они нашли нектара.
После этого на найденные участки отправляются другие пчелы, причем чем больше на данном участке предполагается найти нектара, тем больше пчел летит в этом направлении. А разведчики опять улетают искать другие участки, после чего процесс повторяется.
А теперь представьте, что расположение глобального экстремума - это участок, где больше всего нектара, причем этот участок единственный, то есть в других местах нектар есть, но меньше. А пчелы живут не на плоскости, где для определения месторасположения участков достаточно знать две координаты, а в многомерном пространстве, где каждая координата представляет собой один параметр функции, которую надо оптимизировать. Найденное количество нектара представляет собой значение целевой функции в этой точке (в случае, если мы ищем глобальный максимум, если мы ищем глобальный минимум, то целевую функцию достаточно умножить на -1). Да, наши "неправильные" пчелы могут собирать и отрицательное количество нектара.
Рассмотрим более подробно алгоритм применительно к нахождению экстремумов функции. Далее будем считать, что мы ищем глобальный максимум функции.
В алгоритме каждое решение представляется в виде пчелы, которая знает (хранит) расположение (координаты или параметры многомерной функции) какого-то участка поля, где можно добыть нектар.
На первом шаге алгоритма в точки, описываемые случайными координатами, отправляется некоторое количество пчел-разведчиков (пусть будет S пчел, от слова scout). В зависимости от значения целевой функции, которое определяется координатами пчелы, выделяются два вида перспективных участков на поверхности функции, вблизи которых возможно располагается глобальный максимум. А именно:
- Выбирается n лучших участков, где значения целевой функции больше всех
- Выбирается m так называемых выбранных участков, где значения целевой функции поменьше, чем на лучших участках, но эти участки все-равно являются неплохими с точки зрения значения целевой функции.
Здесь нужно обратить внимание на одну особенность, которая может быть важна при реализации алгоритма. Несколько пчел могут попасть на один и тот же участок (близко друг к другу, размер участка, или возможная близость пчел, задается отдельным параметром). Поэтому можно выделить два варианта поведения:
- Считать, что эти две пчелы нашли два разных пересекающихся участка, и оба этих участка отметить как лучшие или выбранные.
- Считать, что это один участок, центр которого находится в точке, которая соответствует пчеле с большим значением целевой функции.
В реализации, которая будет описана ниже, используется второй вариант поведения, так как он показался менее подверженным застреванию в локальных экстремумах.
В окрестность n лучших участков посылается N пчел, а в окрестность m выбранных участков посылается M пчел, причем на каждый из лучших участков должно приходиться больше пчел, чем на каждый из выбранных участков. Можно сделать так, что чем больше значение целевой функции, тем большее количество пчел будет отправляться на соответствующий участок, а можно N и M сделать фиксированными величинами.
Обратите внимания, что пчелы посылаются не в точности на то место, где пчелы-разведчики нашли перспективные и лучшие места, а в их окрестность, более точно координаты определяются случайным образом. Кроме того, окрестность, которая определяет область, в которую может быть послана пчела, можно уменьшать по мере увеличения номера итерации, чтобы постепенно решение сходилось к самому "кончику" экстремума. Но если область уменьшать слишком быстро, то решение может застрять в локальном экстремуме.
После того как пчелы были отправлены на лучшие и выбранные участки, можно отправить тех же пчел-разведчиков на другие случайные точки.
После всех этих операций снова находятся n лучших и m выбранных участков, на этот раз среди всех пчел из роя, а не только среди разведчиков, и запоминается самое лучшее место на функции, значение больше которого пока не было найдено, это и будет промежуточным решением.
Затем алгоритм повторяется до тех пор пока не сработает какой-нибудь из критериев останова. Критериев останова может быть несколько. Например, если мы знаем значение целевой функции в глобальном экстремуме, то можем повторять алгоритм до тех пор, пока функция не достигнет некоторого значения, близкого к желаемому. Если значение функции в экстремуме неизвестно, то можем повторять шаги алгоритма до тех пор, пока на протяжении какого-то достаточно большого количества итераций найденное решение не будет улучшаться.
Пример итерации
Давайте рассмотрим небольшой пример. Пусть в качестве целевой функции у нас выступает функция
Знак "-" в данном случае стоит, чтобы у функции был глобальный максимум, а не минимум. Глобальный (и единственный) максимум этой функции находится в точке (0; 0), причем f(0, 0) = 0.
Остальные необходимые параметры:
Количество пчел-разведчиков: 10
Количество пчел, отправляемых на лучшие участки: 5
Количество пчел, отправляемых на другие выбранные участки: 2
Количество лучших участков: 2
Количество выбранных участков: 3
Размер области для каждого участка: 10
Пусть разведчики попали на следующие, участки (список отсортирован по убыванию целевой функции):
f(15, 18) = -549
f(-30, -15) = -1125
f(22, -31) = -1445
f(18, 40) = -1924
f(-25, 47) = -2834
f(60, 86) = -10996
f(-91, -99) = -18082
f(17, -136) = -18785
f(-152, -1) = -22501
f(-222, 157) = -73933
Сначала будут выбраны 2 лучшие точки:
f(15, 18) = -549
f(-30, -15) = -1125
Затем будут выбраны другие 3 перспективных участка:
f(22, -31) = -1445
f(18, 40) = -1924
f(-25, 47) = -2834
В окрестности лучших точек будут отправлены по 5 пчел:
Для первой лучшей точки значение координат, которыми ограничивается участок будет:
[15 - 10 = 5; 15 + 10 = 25] для первой координаты
[18 - 10 = 8; 18 + 10 = 28] для второй координаты
И для второй точки:
[-30 - 10 = -40; -30 + 10 = -20] для первой координаты
[-15 - 10 = -25; -15 + 10 = -5] для второй координаты
Аналогично рассчитываются интервалы для выбранных участков:
[12; 32] [-41; -21]
[8; 28] [30; 50]
[-35; 15] [37; 57]
Заметьте, что здесь по каждой из координат размер области одинаков и равен 20, в реальности это не обязательно так.
В каждый из лучших интервалов отправляем по 5 пчел, а на выбранные участки по 2 пчелы. Причем, мы не будем менять положение пчел, нашедших лучшие и выбранные участки, иначе есть вероятность того, что на следующей итерации максимальное значение целевой функции будет хуже, чем на предыдущем шаге.
Пусть теперь на первом лучшем участке мы имеем следующих пчел:
f(15, 18) = -549
f(7, 12) = 193
f(10, 10) = 100
f(16, 24) = 832
f(18, 24) = 900
Как видно, уже среди этих новых точек есть такие, которые лучше, чем предыдущее решение.
Так же поступаем и со вторым лучшим участком, а затем аналогично и с выбранными участками. После чего среди всех новых точек снова отмечаются лучшие и выбранные, а процесс повторяется заново.
Реализация алгоритма на Python
Далее мы рассмотрим пример реализации алгоритма роя пчел на языке Python. Скачать исходники вы можете здесь.
В этом примере используются две дополнительные библиотеки. Matplotlib используется для визуализации данных, а Psyco для ускорения расчета. Библиотека Psyco в данном случае не обязательна, пример будет работать и без нее, но значительно медленнее.
Структура исходников
Архив с исходниками содержит следующие файлы:
pybee.py - основные классы, реализующие алгоритм роя пчел.
beetest.py - основной модуль примера, в котором содержатся все параметры алгоритма. Этот скрипт и нужно запускать.
beeexamples.py - в это модуле содержатся различные классы пчел для разных целевых функций.
beetestfunc.py - вспомогательные функции для визуализации процесса расчета.
Основные классы
В модуле pybee содержатся следующие классы:
floatbee - базовый класс для пчел, положение которых описывается числами с плавающей точкой.
hive - класс улея, внутри которого и происходят основные действия алгоритма по выделению лучших и выбранных участков, а также отправка пчел на нужные позиции.
statistic - вспомогательный класс для сбора статистики по сходимости алгоритма роя пчел. Этот класс накапливает лучшие результаты для каждого шага итерации.
Рассмотрим все эти классы более подробно.
Класс floatbee
Сначала рассмотрим класс floatbee. Это базовый класс, от которого необходимо наследоваться и переопределить один метод, о котором поговорим чуть позже, кроме того в конструкторе нужно определить некоторые члены. А именно:
self.minval
self.maxval
Эти переменные должны быть типа списка (или массив) и содержать столько элементов, сколько аргументов имеет целевая функция, которую необходимо оптимизировать.
self.position хранит в себе одно решение, которое сопоставлено с данной пчелой. В конструкторе рекомендуется заполнять этот список случайными величинами.
self.minval и self.maxval хранят списки, содержащие соответственно минимальные и максимальные значения для координат из self.position.
Допустим, что положение у нас определяется двумя координатами, причем первая координата может изменяться в пределах [-1; 1], а вторая в пределах [-11; 12]. Тогда заполнение этих членов может быть таким:
self.maxval = [1.0, 12.0]
self.position = [random.uniform (self.minval[n], self.maxval[n]) for n in range (2) ]
Таким образом, размеры списков self.position, self.minval и self.maxval всегда должны совпадать.
После заполнение списков этих членов, необходимо перегрузить метод
Именно в нем рассчитывается целевая функция (или здоровье пчелы). Следует особо отметить, что само значение целевой функции не возвращается из этого метода, а присваивается внутри метода члену self.fitness. Сам метод не должен ничего возвращать.
Это сделано для того, чтобы целевая функция считалась только один раз при изменении координат пчелы. Причем метод calcfitness() должен быть обязательно выполнен после любых перемещений пчелы.
Рассмотрим пример. Пусть целевая функция у нас будет f(x, y) = -x^2 - y^2, тогда calcfitness() может выглядеть следующим образом:
...
def calcfitness (self):
"""Расчет целевой функции. Этот метод необходимо перегрузить в производном классе.
Функция не возвращает значение целевой функции, а только устанавливает член self.fitness
Эту функцию необходимо вызывать после каждого изменения координат пчелы"""
self.fitness = 0.0
for val in self.position:
self.fitness -= val * val
Тогда с учетом вышесказанного конструктор для нашей пчелы будет выглядеть следующим образом:
...
def __init__ (self):
self.minval = [-1.0, -11.0]
self.maxval = [1.0, 12.0]
self.position = [random.uniform (self.minval[n], self.maxval[n]) for n in range (2) ]
self.calcfitness()
С точки зрения пользователя больше про класс пчел ничего знать не обязательно. Оставшиеся члены класса floatbee будут кратко рассмотрены по мере их упоминания при разборе основного алгоритма.
Класс hive
Основные шаги алгоритма роя пчел реализованы внутри класса hive (улей), поговорим о нем подробнее.
Для начала рассмотрим параметры конструктора
...
def __init__ (self, scoutbeecount, selectedbeecount, bestbeecount, \
selsitescount, bestsitescount, \
range_list, beetype):
Как видите, в конструктор передается 7 параметров (не считая self):
scoutbeecount - количество пчел-разведчиков
selectedbeecount - количество пчел, посылаемых на каждый из выбранных (не лучших) участков. Имеется в виду, сколько пчел будет отправлено на один участок.
bestbeecount - количество пчел, посылаемых на каждый из лучших участков.
selsitescount - количество выбранных (перспективных, но не лучших) участков.
bestsitescount - количество лучших участков.
range_list - список, элементы которого определяют размеры выбранных и лучших участков по каждой координате (об этом чуть ниже)
beetype - класс пчел, производный от floatbee, который используется в алгоритме.
С первыми пятью параметрами и последним думаю все понятно, рассмотрим параметр range_list, который представляет собой список размеров областей, куда посылаются пчелы. Его роль в алгоритме проще показать на примере.
Пусть у нас положение участков определяется двумя координатами (целевая функция имеет два параметра, или пчелы "живут" в двумерном мире), тогда список (или массив) range_list должен иметь два элемента. Пусть это будут
[1.0, 2.0]
Это значит, что при отправке пчелы в область какой-то точки (x; y), значение ее первой координаты будет случайным образом выбрано из интервала [x - 1.0; x + 1.0], а значение второй координаты - [y - 2.0; y + 2.0]. То есть, если мы отправим пчелу в область точки (10.0, 20.0), то в реальности получим координаты, которые будут лежать в пределах от 9.0 до 11.0 для первой координаты и от 18.0 до 22.0 для второй.
Кстати, для отправки пчелы в окрестность точки в классе floatbee есть метод
в котором
otherpos - точка, в окрестность которой посылается пчела
range_list - тот же самый список размеров окрестностей, про который мы только что говорили.
Возвращаемся к конструктору класса hive. Рассмотрим его код
...
def __init__ (self, scoutbeecount, selectedbeecount, bestbeecount, \
selsitescount, bestsitescount, \
range_list, beetype):
self.scoutbeecount = scoutbeecount
self.selectedbeecount = selectedbeecount
self.bestbeecount = bestbeecount
self.selsitescount = selsitescount
self.bestsitescount = bestsitescount
self.beetype = beetype
self.range = range_list
# Лучшая на данный момент позиция
self.bestposition = None
# Лучшее на данный момент здоровье пчелы (чем больше, тем лучше)
self.bestfitness = -1.0e9
# Начальное заполнение роя пчелами со случайными координатами
beecount = scoutbeecount + selectedbeecount * selsitescount + bestbeecount * bestsitescount
self.swarm = [beetype() for n in xrange (beecount)]
# Лучшие и выбранные места
self.bestsites = []
self.selsites = []
self.swarm.sort (floatbee.sort, reverse = True)
self.bestposition = self.swarm[0].getposition()
self.bestfitness = self.swarm[0].fitness
Во-первых, в нем сохраняются все передаваемые параметры. Во-вторых, создается член self.bestposition, который хранит в себе лучшее на данный момент решение.
Значение целевой функции для лучшего на данный момент решения хранится в члене self.bestfitness.
Затем создается рой пчел. Общее количество пчел в нем равно
То есть сумма количества разведчиков, количества пчел посылаемых на один выбранный участок, умноженное на количество выбранных участков, и количества пчел, посылаемых на один из лучших участков, умноженное на количество лучших участков.
Затем просто заполняется список члена self.swarm (рой):
Напомню, что в конструкторе все параметры пчелы должны инициализироваться случайным образом, поэтому получается, что при создании роя пчел, все они выступают в роли пчел-разведчиков, которых отправляют на случайные точки. С точки зрения алгоритма это не обязательно должно быть так. Можно в первый раз отправить только заданное количество пчел-разведчиков, а пчел, предназначенных для лучших и выбранных участков, отправлять на следующих итерациях. Но в данном случае в самом начале на случайные места отправляются все пчелы, участвующие в алгоритме.
После того как рой создан, он сортируется по убыванию целевой функции у каждой пчелы. В качестве функции сравнения передается метод sort() из класса floatbee.
После сортировки лучшим будет решение у пчелы, находящейся в самом начале списка. Значение целевой функции для данной пчелы сохраняется в член self.bestfitness, а в член self.bestposition сохраняется копия (!) координат лучшей пчелы. Для получения копии координат используется метод getposition() из класса floatbee:
...
def getposition (self):
"""Вернуть копию (!) своих координат"""
return [val for val in self.position]
Приступаем к самому интересному, к методу, где и содержатся действия для основных шагов алгоритма.
Для выполнения одной итерации алгоритма роя пчел необходимо из экземпляра класса hive вызвать метод
Рассмотрим этот метод более подробно.
Этот метод состоит из двух логических этапов. Сначала выбираются лучшие и выбранные участки. Выбор лучших участков происходит следующим образом:
...
def nextstep (self):
# Выбираем самые лучшие места и сохраняем ссылки на тех, кто их нашел
self.bestsites = [ self.swarm[0] ]
curr_index = 1
for currbee in self.swarm [curr_index: -1]:
# Если пчела находится в пределах уже отмеченного лучшего участка, то ее положение не считаем
if currbee.otherpatch (self.bestsites, self.range):
self.bestsites.append (currbee)
if len (self.bestsites) == self.bestsitescount:
break
curr_index += 1
...
Пчелы, нашедшие лучшие участки помещаются в список self.bestsites. Во-первых, туда помещается пчела, находящаяся в начале списка, а затем происходит перебор остальных пчел до тех пор пока не будет отобрано нужное количество. Причем пропускаются пчелы, которые находятся в одном участке с пчелой, которая уже находится в списке self.bestsites. curr_index хранит номер пчелы в списке, которую будем проверять следующей.
Проверка того является ли участок, найденный пчелой новым или какая-то пчела уже находится поблизости, происходит внутри метода otherpatch() класса floatbee.
...
def otherpatch (self, bee_list, range_list):
"""Проверить находится ли пчела на том же участке, что и одна из пчел в bee_list.
range_list - интервал изменения каждой из координат"""
if len (bee_list) == 0:
return True
for curr_bee in bee_list:
position = curr_bee.getposition()
for n in xrange ( len (self.position) ):
if abs (self.position[n] - position[n]) > range_list[n]:
return True
return False
В данном случае в качестве bee_list передается список лучших пчел self.bestsites, а в качестве range_list все тот же список размеров окрестностей. Участок, найденный пчелой, считается новым, если в списке bee_list нет пчелы, расстояние до которой по каждой из координат не превышает соответствующего размера из range_list.
После нахождения таким образом лучших участков аналогично отмечаем выбранные участки.
...
def nextstep (self):
...
self.selsites = []
for currbee in self.swarm [curr_index: -1]:
if currbee.otherpatch (self.bestsites, self.range) and currbee.otherpatch (self.selsites, self.range):
self.selsites.append (currbee)
if len (self.selsites) == self.selsitescount:
break
Пчелы с выбранных участков сохраняются в список self.selsites.
После того как мы отметили лучшие и выбранные участки, отправим пчел на соответствующие позиции.
...
def nextstep (self):
...
# Номер очередной отправляемой пчелы. 0-ую пчелу никуда не отправляем
bee_index = 1
for best_bee in self.bestsites:
bee_index = self.sendbees (best_bee.getposition(), bee_index, self.bestbeecount)
for sel_bee in self.selsites:
bee_index = self.sendbees (sel_bee.getposition(), bee_index, self.selectedbeecount)
# Оставшихся пчел пошлем куда попадет
for curr_bee in self.swarm[bee_index: -1]:
curr_bee.gotorandom()
self.swarm.sort (floatbee.sort, reverse = True)
self.bestposition = self.swarm[0].getposition()
self.bestfitness = self.swarm[0].fitness
За отправку пчел отвечает метод sendbees() класса hive. Суть ее состоит в том, что она отправляет заданное количество пчел, пропуская тех, которые уже находятся среди лучших и выбранных пчел. Я не буду приводить здесь этот метод, так он довольно простой и для понятия алгоритма не так важен. Но нужно сказать, что внутри sendbees() вызывается метод goto() класса floatbee. Его мы рассмотрим поподробнее.
...
def goto (self, otherpos, range_list):
"""Перелет в окрестность места, которое нашла другая пчела. Не в то же самое место! """
# К каждой из координат добавляем случайное значение
self.position = [otherpos[n] + random.uniform (-range_list[n], range_list[n]) \
for n in xrange (len (otherpos) ) ]
# Проверим, чтобы не выйти за заданные пределы
self.checkposition()
# Расчитаем и сохраним целевую функцию
self.calcfitness()
Здесь сначала заполняется список новых координат, которые складываются из точки, в которую отправляют пчелу и случайной величины в интервале от -range_list[n] до range_list[n].
Затем вызывается метод checkposition(), который корректирует координаты, если они выходят за заданные пределы (помните списки minval и maxval, про которые мы говорили при обсуждении конструктора пчел?)
...
def checkposition (self):
"""Скорректировать координаты пчелы, если они выходят за установленные пределы"""
for n in range ( len (self.position) ):
if self.position[n] < self.minval[n]:
self.position[n] = self.minval[n]
elif self.position[n] > self.maxval[n]:
self.position[n] = self.maxval[n]
После того как были отправлены пчелы на лучшие и выбранные места, оставшихся пчел из улея отправляем на случайные координаты. Затем все пчелы опять сортируются по убыванию целевой функции и сохраняются лучшие позиции и лучшее значение целевой функции.
Метод nextstep() вызывается пользователем до тех пор пока не будет выполнено одно из условий останова, но об этом мы поговорим, когда будем разбирать примеры использования алгоритма роя пчел.
Класс statistic
В модуле pybee есть еще один класс, который не используется в алгоритме непосредственно, но который может помочь в отладке и визуализации результатов. Это класс statistic, который сохраняет найденное решение для каждого шага итерации. Причем, один экземпляр класса statistic можно использовать для нескольких независимых запусков алгоритма. Это может понадобиться для того, чтобы посмотреть, например, как сходятся параметры при усреднении по нескольким запускам.
Рассмотрим конструктор класса statistic и обсудим способ хранения данных в нем.
""" Класс для сбора статистики по запускам алгоритма"""
def __init__ (self):
# Индекс каждого списка соответствует итерации.
# В элементе каждого списка хранится список значений для каждого запуска
# Добавлять надо каждую итерацию
# Значения целевой функции в зависимости от номера итерации
self.fitness = []
# Значения координат в зависимости от итерации
self.positions = []
# Размеры областей для поискарешения в зависимости от итерации
self.range = []
В классе содержатся три списка, которые хранят значения целевой функции, координат и размеров областей. Хранятся значения следующим образом (будем рассматривать на примере self.positions). self.positions хранит список, первый индекс которого обозначает номер запуска алгоритма (начиная с 0). Внутри каждого элемента хранится список, каждый элемент которого обозначает номер итерации алгоритма. А внутри этого второго списка хранится список координат, лучших на данную итерацию. То есть, чтобы получить k-ую координату, которая была при m-ой итерации при n-ом запуске алгоритма, необходимо написать следующее выражение (считаем, что stat - экземпляр класса statistic):
Аналогично со списком range. Список fitness немного проще из-за того, что целевая функция представляет собой число, а не список, то есть индекса k у нее нет.
Для каждой итерации алгоритма (после каждого вызова метода nextstep() класса hive) необходимо вызвывать метод add(), который добавляет результат в статистику:
Не буду приводить исходный код этой функции, так как для понимания алгоритма этого не требуется, в нем просто сохраняются в соответствующих списках значения целевой функции, координаты и интервал изменения диапазонов координат согласно структуре, которую мы только что рассмотрели.
Также я не буду приводить здесь методы, предназначенные для вывода таблиц целевой функции и координат. Их использование будет ясно из примеров, а исходный код вы можете посмотреть, скачал архив с исходниками.
Пример работы алгоритма
Вот мы и подошли к самому интересному разделу, где будет много цветных картинок. :)
В качестве примеров в исходниках используются пять целевых функций, описанных в [3], а так же еще одна дополнительная. Разумеется, все шесть функций мы здесь рассматривать не будем, рассмотрим только одну из них.
В качестве примеров рассмотрим только класс пчел, производный от floatbee, остальные классы будут устроены аналогичным образом. Все классы пчел для различных целевых функций описаны в файле beeexamples.py.
Итак, пусть наша целевая функция имеет вид (так называемая гиперсфера)
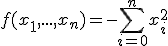
Максимум такой функции находится в точке, когда все координаты равны 0. Рассмотрим класс пчелы для этой целевой функции.
"""Функция - сумма квадратов по каждой координате"""
# Количество координат
count = 20
def __init__ (self):
pybee.floatbee.__init__ (self)
self.minval = [-150.0] * spherebee.count
self.maxval = [150.0] * spherebee.count
self.position = [random.uniform (self.minval[n], self.maxval[n]) for n in xrange (spherebee.count) ]
self.calcfitness()
def calcfitness (self):
"""Расчет целевой функции. Этот метод необходимо перегрузить в производном классе.
Функция не возвращает значение целевой функции, а только устанавливает член self.fitness
Эту функцию необходимо вызывать после каждого изменения координат пчелы"""
self.fitness = 0.0
for val in self.position:
self.fitness -= val * val
@staticmethod
def getstartrange ():
return [150.0] * spherebee.count
@staticmethod
def getrangekoeff ():
return [0.98] * spherebee.count
Как видно, этот класс пчелы довольно компактный, разберем его составные части. Все рассматриваемые здесь классы пчел (в том числе и не рассматриваемые, но находящиеся в исходниках) кроме обязательных членов и методов, необходимых для работы алгоритма (о которых мы уже говорили) будут обладать дополнительными членами и методами, необходимыми для запуска примеров. Это сделано для того, чтобы в примерах можно было бы легко менять класс используемых пчел, а также визуализировать данные, не заботясь о количестве используемых координат. Все это мы обсудим подробнее.
Обратите внимание на переменную count внутри класса, она обозначает количество координат (n) нашей гиперсферы, в других классах пчел так же используется эта переменная.
Начнем с конструктора. В нем для порядка сначала вызывается конструктор базового класса floatbee, затем создаются три списка:
- Список минимальных значений для каждой из координат (self.minval).
- Список максимальных значений (self.maxval).
- Список текущих координат (self.position), заполненный случайными величинами.
После заполнения координатами списка self.position вызывается метод self.calcfitness() для вычисления целевой функции, используя текущие координаты. Метод calcfitness() не должен вызывать вопросов.
Затем идут два очень простых статических метода, которые облегчают запуск примеров независимо от того какой класс пчел используется. Метод getstartrange() используется для задания начальных размеров для каждой из областей. Именно этот список и передается в конструктор класса hive.
Кроме того есть еще один статический метод getrangekoeff(), возвращающий список коэффициентов, определяющих во сколько раз будут уменьшаться размеры областей при необходимости. В данном примере эти коэффициенты равны 0.98, т.е. каждый раз, когда надо будет сузить область поиска, элементы списка range класса hive будут умножаться на 0.98.
Перейдем теперь к рассмотрению скрипта beetest.py, из которого и происходит запуск алгоритма. Этот скритп требует, чтобы был установлен пакет pylab (он же Matplotlib), который используется для визуализации данных. Кроме того очень желательно, чтобы был установлен пакет psyco, который существенно ускоряет расчет, хотя и без него скрипт будет работать.
Думаю, что нет смысла описывать очень подробно каждую строку из beetest.py, рассмотрим только ключевые моменты.
Сначала создается класс для сбора статистики
Параметры алгоритма роя пчел задаются после после комментария
## Параметры алгоритма
###################################################
В первую очередь задается класс используемых пчел. Для этого надо раскомментарить одну из следующих строк:
#beetype = beeexamples.dejongbee
#beetype = beeexamples.goldsteinbee
#beetype = beeexamples.rosenbrockbee
#beetype = beeexamples.testbee
#beetype = beeexamples.funcbee
Затем идет задание других параметров алгоритма, назначение которых, думаю, понятно из комментариев к ним:
scoutbeecount = 300
# Количество пчел, отправляемых на выбранные, но не лучшие участки
selectedbeecount = 10
# Количество пчел, отправляемые на лучшие участки
bestbeecount = 30
# Количество выбранных, но не лучших, участков
selsitescount = 15
# Количество лучших участков
bestsitescount = 5
А вот дальше располагаются параметры, о которых нужно рассказать поподробнее.
runcount = 1
# Максимальное количество итераций
maxiteration = 1000
# Через такое количество итераций без нахождения лучшего решения уменьшим область поиска
max_func_counter = 10
runcount - это количество независимых запусков алгоритма. Так как алгоритм во многом зависит от случайных величин, то многократный запуск, а также усреднение по всем запускам будет более наглядно показывать сходимость алгоритма, чем запуск только один раз. Хотя в данном случае по умолчанию алгоритм запускается именно один раз.
maxiteration - это максимальное количество итераций алгоритма. В данном случае это единственный критерий останова. Это сделано для того, чтобы было проще усреднять результаты работы по нескольким запускам. Если бы был введен еще другой критерий останова, то в классе для сбора статистика для каждого запуска списки с результатами были бы разной длины.
max_func_counter определяет через сколько итераций, которые не дают лучшего решения, будут уменьшаться размеры областей для поиска решения. То есть в данном случае, если в течение 10 итераций не будет найдено решение лучше, чем было до этого, то область, задаваемая списком hive.range, будет уменьшена в соответствии со списком, возвращаемым статическим методом getrangekoeff() класса пчелы, то есть в данном случае размер будет умножен на 0.98.
Рассмотрим еще некоторые частки кода внутри цикла по количеству запусков алгоритма. Во-первых, создается класс улея:
selsitescount, bestsitescount, \
beetype.getstartrange(), beetype)
Сразу же добавляем текущее лучшее решение в статистику
Создаются необходимые переменные для подсчета количества неудачных итераций (когда более хорошее решение не было найдено)
best_func = -1.0e9
# Количество итераций без улучшения целевой функции
func_counter = 0
И основной цикл по всем итерациям. Про закомментаренные строки мы поговорим чуть позже
currhive.nextstep ()
stat.add (runnumber, currhive)
if currhive.bestfitness != best_func:
# Найдено место, где целевая функция лучше
best_func = currhive.bestfitness
func_counter = 0
# Обновим рисунок роя пчел
#plotswarm (currhive, 0, 1)
print "\n*** iteration %d / %d" % (runnumber + 1, n)
print "Best position: %s" % (str (currhive.bestposition) )
print "Best fitness: %f" % currhive.bestfitness
else:
func_counter += 1
if func_counter == max_func_counter:
# Уменьшим размеры участков
currhive.range = [currhive.range[m] * koeff[m] for m in xrange ( len (currhive.range) ) ]
func_counter = 0
print "\n*** iteration %d / %d (new range)" % (runnumber + 1, n)
print "New range: %s" % (str (currhive.range) )
print "Best position: %s" % (str (currhive.bestposition) )
print "Best fitness: %f" % currhive.bestfitness
#if n % 10 == 0:
#plotswarm (currhive, 2, 3)
Итак, n здесь соответствует номеру итерации (начиная с 0). Сначала вызывается метод nextstep() для новой итерации, а затем результат добавляется в статистику. Потом, если на данной итерации было найдено лучшее решение, то оно сохраняется, а в консоль выводится номер итерации, новое найденное решение и значение целевой функции.
Если на данной итерации новое решение не найдено, то увеличивается счетчик func_counter для неудачных итераций, и если его значение стало равно max_func_counter (которое мы задали выше), то происходит сужение областей для каждой из координат. После чего, опять же, выводится в консоль номер итерации, новые диапазоны, лучшие на данный момент решение и значение целевой функции.
Все остальные строки исходника, в том числе, идущие и после цикла по итерациям, предназначены для наглядного представления результатов работы алгоритма. О них мы сейчас и поговорим.
Все функции для визуализации с помощью библиотеки pylab находятся в файле beetestfunc.py.
Во-первых, это функция plotswarm(), которая на плоскости отмечает расположение каждой пчелы. В качестве первого параметра в нее необходимо передать экземпляр класса hive. Второй и третий параметры - номера индексов координат пчелы, отображаемые на плоскости. Так как мы рисуем пчел на плоскости, а у целевой функции может быть больше параметров (координат пчелы), то мы можем отобразить только две координаты, которые и задаются с помощью этих двух параметров.
По умолчанию отображение пчел отключено для ускорения счета, но вы можете его включить, причем обновление рисунка может происходить в двух случаях: если было найдено более хорошее решение, и может быть обновление на каждой 10-ой итерации. Для первого случая раскомментарьте строку
после комментария
Во втором случае раскомментарьте две строки
#beetestfunc.plotswarm (currhive, 2, 3)
Надо сразу отметить, что для простоты и наглядности скрипта отображение роя пчел происходит в том же потоке (в смысле thread), что и выполнение основного алгоритма, поэтому обновление картинки может "виснуть", если переключиться на другое приложение, при этом сам алгоритм будет работать.
На анимации внизу вы можете увидеть как пчелы постепенно скапливаются вокруг одного лучшего решения. На этом рисунке красные точки - пчелы, нашедшие лучшие решения, желтый точки - выбранные решения, а черные точки - остальные пчелы, включая пчел-разведчиков, которые располагаются случайным образом.
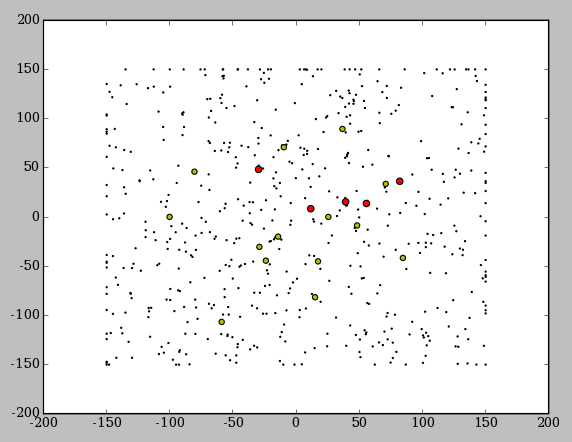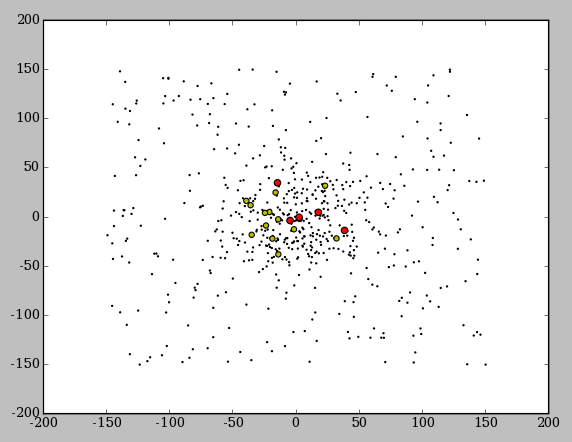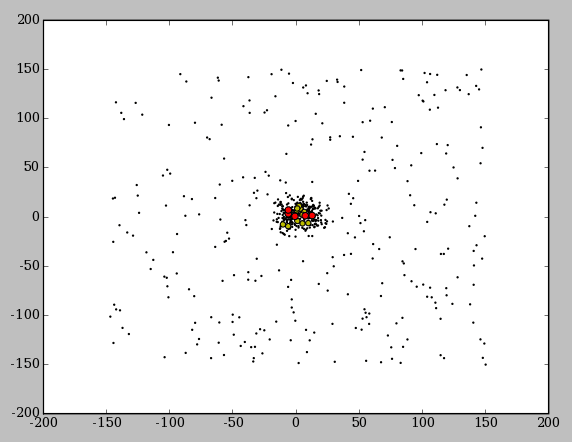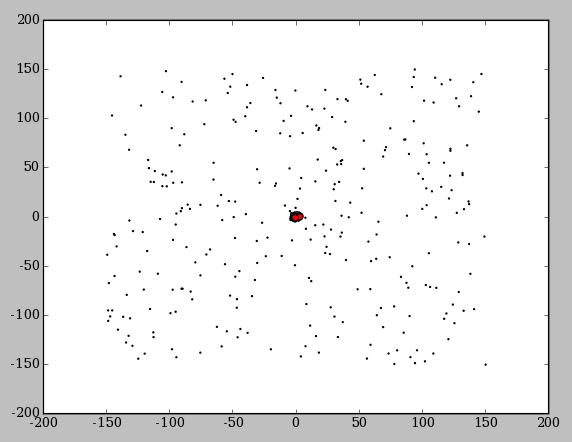
В данном примере использовался класс пчел spherebee с количеством координат count = 4.
В конце расчета выводятся графики сходимости решения и значения целевой функции в зависимости от номера итерации. Для большей наглядности на следующих картинках приведены примеры из другой целевой функции (класс funcbee, который здесь не описан).
Рост целевой функции при одном запуске алгоритма:
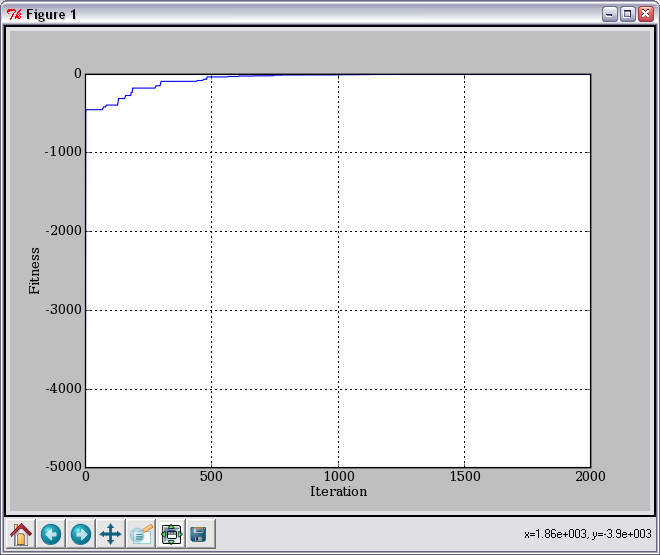
Рост целевой функции, усредненный по 10 запускам алгоритма:
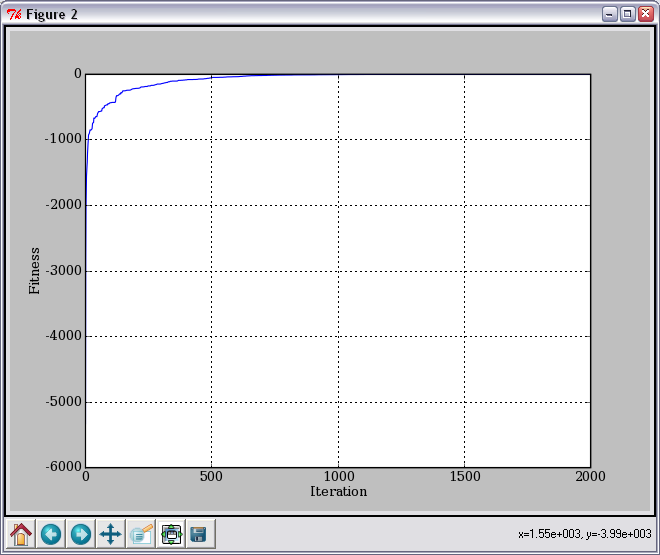
Сходимость решений при одном запуске алгоритма:
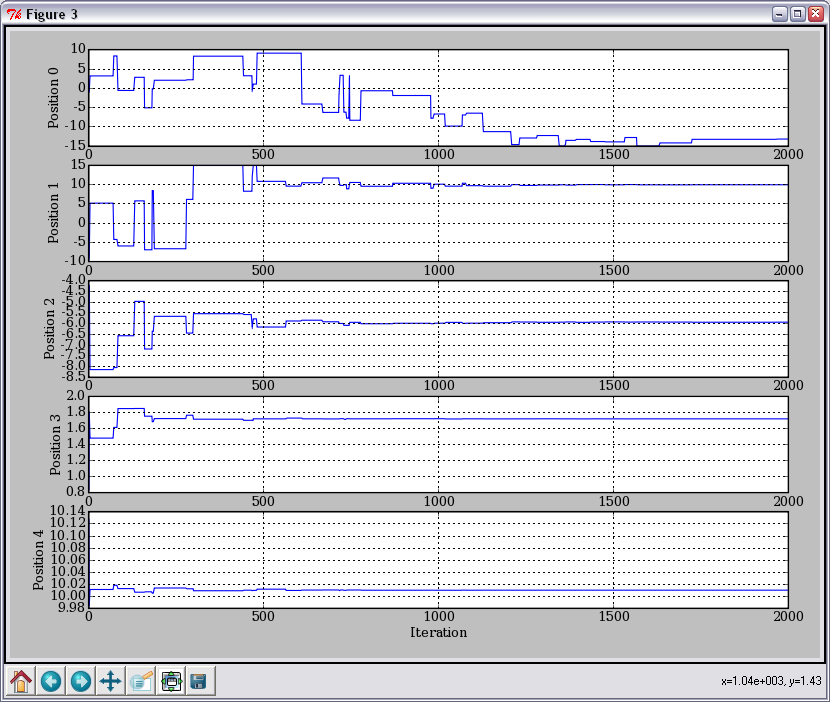
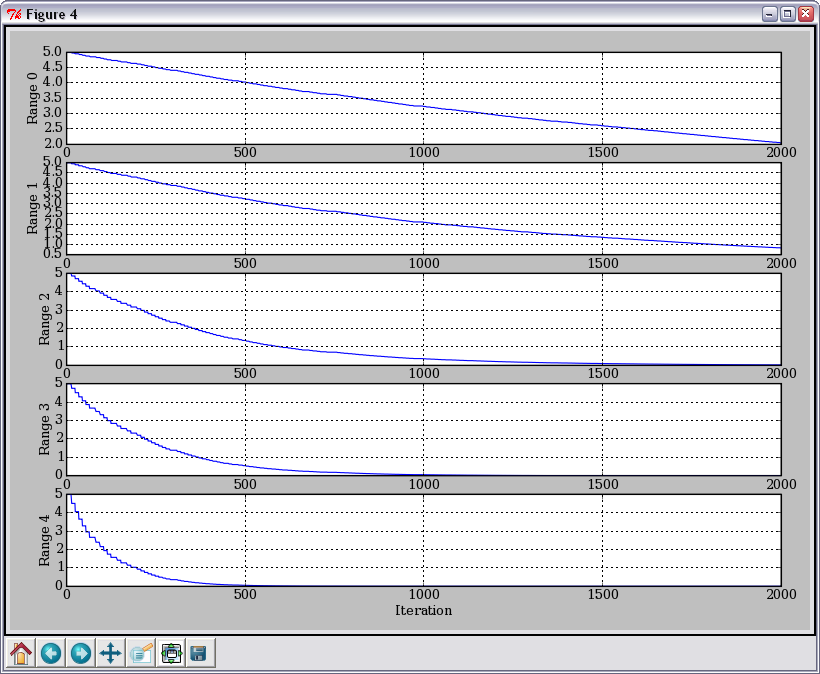
Уменьшение размеров областей для каждой из координат:
Заключение
Мы с вами рассмотрели алгоритм пчел для нахождений глобального экстремума функции и заодно посмотрели возможную реализацию на языке Python. В исходниках, которые вы можете скачать, есть 6 классов пчел для различных целевых функций, 5 из этих функций которых в качестве примеров приводятся в [3]. Судя по этой же статье, алгоритм пчел намного быстрее сходится к правильному решению чем, например, генетический алгоритм.
Очень надеюсь, что удалось доходчиво объяснить суть алгоритма и пример реализации, если есть вопросы, пишите в комментарии.
Ссылки
[1] Pham DT, Ghanbarzadeh A, Koc E, Otri S, Rahim S and Zaidi M. The Bees Algorithm. Technical Note, Manufacturing Engineering Centre, Cardiff University, UK, 2005
[2] D. Karaboga, AN IDEA BASED ON HONEY BEE SWARM FOR NUMERICAL OPTIMIZATION,TECHNICAL REPORT-TR06,Erciyes University, Engineering Faculty, Computer Engineering Department 2005.
[3] The Bees Algorithm – A Novel Tool for Complex Optimisation Problems D.T. Pham, A. Ghanbarzadeh, E. Koc, S. Otri , S. Rahim , M. Zaidi Manufacturing Engineering Centre, Cardiff University, Cardiff CF24 3AA, UK. Скачать эту статью можно здесь.
Вы можете подписаться на новости сайта через RSS, Группу Вконтакте или Канал в Telegram.
