Алгоритм роя частиц. Описание и реализации на языках Python и C#
Содержание
- Введение
- Описание алгоритма
- Реализация алгоритма роя частиц на языке Python
- Примеры минимизируемых функций
- Реализация алгоритма роя частиц на C#
- Заключение
- Комментарии
В этой статье описывается алгоритм глобальной оптимизации, который называется алгоритм (или метод) роя частиц, а также приводятся два примера его реализации: на языках Python и C#.
Введение
При решении многих задач приходится иметь дело с оптимизацией функций (которую называют целевой функцией) в зависимости от многих параметров. В качестве такой функции, например, может быть количество пересечений дорожек на печатной плате в системе автоматизированного проектирования в зависимости от расположения элементов на плате, или количество ошибок, допущенных нейронной сетью при обучении в зависимости от ее весовых коэффициентов. Оптимизация используется при составлении расписаний, в различных математических задачах, например, задаче коммивояжора или задача об N ферзях и во многих других областях.
Большая Советская Энциклопедия дает следующее определение слову оптимизация:
Оптимизация (от лат. optimum — наилучшее), процесс нахождения экстремума (глобального максимума или минимума) определённой функции или выбора наилучшего (оптимального) варианта из множества возможных.
Для простоты в дальнейшем будем считать, что нам надо найти минимум целевой функции от нескольких аргументов дробного типа. Если у функции есть только один минимум (там, где производная функции обращается в ноль, а значение второй производной положительно), то для такого случая хорошо работают различные градиентные методы или алгоритм Нелдера-Мида, который не требует расчета производной функции. Если же у функции несколько экстремумов, то градиентные алгоритмы остановятся на ближайшем экстремуме, и не факт, что этот экстремум будет лучшим на всей области, где мы ищем решение. Или, другими словами, градиентные методы найдут локальный экстремум, а нам хотелось бы найти глобальный.
В качестве примера на следующем рисунке показана одномерная функция Растригина (о ней будет сказано ниже в разделе с примерами). Наша цель будет найти глобальный минимум, который расположен в точке с координатой x1 = 0.
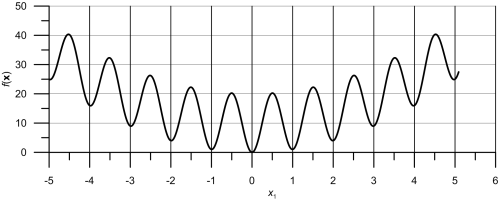
Для решения таких задач было предложено довольно много интересных алгоритмов, про некоторые из них я уже писал - это генетический алгоритм и алгоритм пчел. Алгоритм роя частиц, которому посвящена эта статья, тоже относится к стохастическим алгоритмам с одновременным поиском решения сразу по всей области поиска.
Описание алгоритма
Алгоритм роя частиц был предложен в 1995 году Джеймсом Кеннеди (Kennedy) и Расселом Еберхартом (Eberhart). Их статью (Kennedy, J.; Eberhart, R. (1995). "Particle Swarm Optimization". Proceedings of IEEE International Conference on Neural Networks IV, pp.1942-1948), в которой впервые упоминается данный алгоритм, в формате PDF можно скачать здесь.
Идея алгоритма была частично заимствована из исследований поведения скоплений животных (косяков рыб, стай птиц и т.п.), модель была немного упрощена и добавлены элементы поведения толпы людей, поэтому, в отличие, например, от алгоритма пчел агенты алгоритма (возможные решения) и были названы нейтрально - частицы. Кстати, в своей статье Кеннеди и Еберхарт почти описали алгоритм пчел, но отбросили его и не стали развивать.
Блок-схема алгоритма выглядит следующим образом:
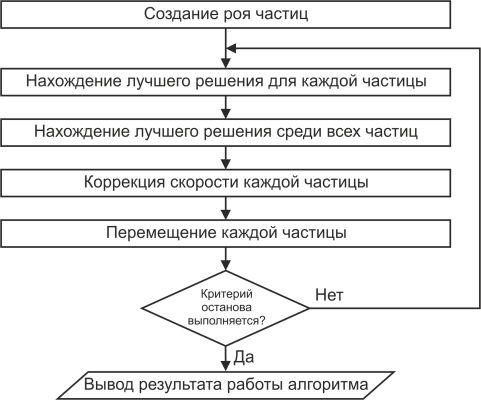
Чтобы понять алгоритм роя частиц, представьте себе n-мерное пространство (область поиска), в котором рыщут частицы (агенты алгоритма). В начале частицы разбросаны случайным образом по всей области поиска и каждая частица имеет случайный вектор скорости. В каждой точке, где побывала частица, рассчитывается значение целевой функции. При этом каждая частица запоминает, какое (и где) лучшее значение целевой функции она лично нашла, а также каждая частица знает где расположена точка, являющаяся лучшей среди всех точек, которые разведали частицы. На каждой итерации частицы корректируют свою скорость (модуль и направление), чтобы с одной стороны быть поближе к лучшей точке, которую частица нашла сама (авторы алгоритма назвали этот аспект поведения "ностальгией"), и, в то же время, приблизиться к точке, которая в данный момент является глобально лучшей. Через некоторое количество итераций частицы должны собраться вблизи наиболее хорошей точки, хотя возможно, что часть частиц останется где-то в относительно неплохом локальном экстремуме, но главное, чтобы хотя бы одна частица оказалась вблизи глобального экстремума.
Самое интересное в алгоритме - это коррекция скорости, именно от этого шага зависит сходимость алгоритма. В первоначальном виде алгоритма коррекция скорости выглядела следующим образом:
vi,t+1 = vi,t + φp rp (pi - xi, t) + φg rg (gi - xi, t)
Здесь vi, t – i-я компонента скорости при t-ой итерации алгоритма xi, t – i-я координата частицы при t-ой итерации алгоритма pi – i-я координата лучшего решения, найденного частицей gi – i-я координата лучшего решения, найденного всеми частицами rp, rg – случайные числа в интервале (0, 1) φp, φg – весовые коэффициенты, которые надо подбирать под конкретную задачу
Затем корректируем текущую координату каждой частицы
xi, t + 1 = xi, t + vi,t+1
После этого рассчитываем значение целевой функции в каждой новой точке, каждая частица проверяет, не стала ли новая координата лучшей среди всех точек, где она побывала. Затем среди всех новых точек проверяем, не нашли ли мы новую глобально лучшую точку, и, если нашли, запоминаем ее координаты и значение целевой функции в ней.
Модификации алгоритма
Формула для коррекции скорости частиц является сутью алгоритма, на подбор коэффициентов φp и φg были направлены многие исследования, также были предложены модифицированные алгоритмы роя частиц, коротко рассмотрим некоторые из них.
Учет инерции
Одна из модификаций алгоритма состоит в том, чтобы добавить еще один весовой коэффициент ω (t) перед текущей скоростью (коэффициент инерции), благодаря которому скорость изменяется более плавно.
vi,t+1 = ω(t) vi,t + φp rp (pi - xi, t) + φg rg (gi - xi, t)
Этот коэффициент может быть константой, а может зависеть от номера итерации t, например, линейно уменьшаться, начиная от небольшой величины, меньшей 1, и до какой-то другой величины, отличной от нуля. В статье A Comparison of Particle Swarm Optimization Algorithms Based on Run-Length Distributions приводился пример, где ω(t) изменяется от 0.9 до 0.4.
Канонический алгоритм
Один из самых распространенных вариантов алгоритма вводит нормировку коэффициентов φp и φg, чтобы сходимость не так сильно зависела от их выбора.
vi,t+1 = χ [vi,t + φp rp (pi - xi, t) + φg rg (gi - xi, t)],
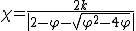 ,
,φ = φp + φg,
φ > 4
коэффициент k должен лежать в интервале (0, 1).
Именно такой алгоритм и реализован в исходниках, прилагающихся, к этой статье.
Существуют и другие модификации алгоритма, которые, например, учитывают не точку, которую каждая частица запомнила, как лучшую, а точку, которая стала лучшей для самой частицы и ближайших ее соседей. Но на других вариантах алгоритма подробно останавливаться не будем.
Немного о грустном, о недостатках алгоритма. Во-первых, он обладает всеми недостатками, что и другие стохастические алгоритмы оптимизации - не гарантирована сходимость алгоритма при конечном числе частиц, отсюда и увеличение необходимого количества расчетов целевой функции (но, разумеется, меньше, чем у простого перебора), и, что характерно именно для этого алгоритма, - это ориентация на одну лучшую точку, что увеличивает вероятность остановки алгоритма в неплохом, но не глобальном минимуме. Но как плюс алгоритма - это его понятность и возможность быстро перестроить алгоритм на другую формулу для расчета скорости частиц. Кроме того, он довольно эффектно выглядит при визуализации. :)
А теперь перейдем к реализации алгоритма.
Реализация алгоритма роя частиц на языке Python
В одном архиве расположены исходники сразу для двух языков - Python (папка python) и C# (папка .net).
Для начала рассмотрим реализацию метода роя частиц на языке Python, поскольку этот язык очень лаконичный и позволяет наглядно показать работу алгоритма. Для запуска примеров должна быть установлена библиотека Numpy.
Реализация алгоритма роя частиц содержится в пакете particleswarm, который написан таким образом, чтобы пользователю этого пакета нужно было бы только написать минимизируемую функцию и задать границы ее определения, не вдаваясь в подробности работы алгоритма. Разберем структуру пакета particleswarm подробнее.
Этот пакет содержит два класса:
- Particle описывает поведение частицы на каждом шаге итерации.
- Swarm - это абстрактный базовый класс, в котором необходимо определить целевую функцию. Именно с классом, производным от Swarm работает пользователь.
На следующей диаграмме показаны основные элементы классов Particle и Swarm.
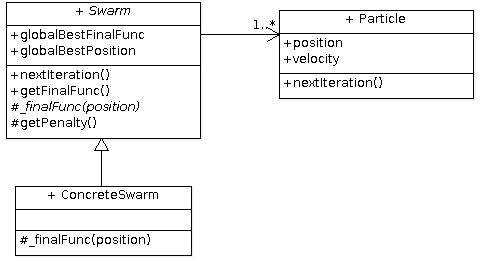
Прежде чем рассматривать внутреннюю работу пакета particleswarm разберемся с тем, как этот пакет должен использовать пользователь.
Пользователь должен создать класс, производный от Swarm (на диаграмме это ConcreteSwarm) и определить метод _finalFunc(), который должен вернуть значение целевой функции в зависимости от переданного параметра position - координат, где нужно рассчитать значение.
Все координаты в алгоритме представляют собой массив чисел, размерность которого равна размерности задачи. Если быть точнее, то используется класс numpy.array, чтобы можно было использовать удобные операции с массивами без необходимости организовывать перебор значений списков.
Конструктор класса Swarm выглядит следующим образом:
swarmsize,
minvalues,
maxvalues,
currentVelocityRatio,
localVelocityRatio,
globalVelocityRatio):
"""
swarmsize - размер роя (количество частиц)
minvalues - список, задающий минимальные значения для каждой координаты частицы
maxvalues - список, задающий максимальные значения для каждой координаты частицы
currentVelocityRatio - общий масштабирующий коэффициент для скорости
localVelocityRatio - коэффициент, задающий влияние лучшей точки,
найденной каждой частицей, на будущую скорость
globalVelocityRatio - коэффициент, задающий влияние лучшей точки,
найденной всеми частицами, на будущую скорость
"""
...
Если использовать использовать терминологию, описываемую выше, то currentVelocityRatio - это коэффициент k, localVelocityRatio - это φp, а globalVelocityRatio - это φg. Так как используется каноническая версия алгоритма, то должно выполняться условие localVelocityRatio + globalVelocityRatio > 4.
Допустим, что мы хотим минимизировать вот такую простую функцию:
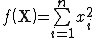
Класс роя для такой функции может выглядеть следующим образом (в исходниках это файл swarm_x2.py):
# -*- coding: UTF-8 -*-
from particleswarm.swarm import Swarm
class Swarm_X2 (Swarm):
def __init__ (self,
swarmsize,
minvalues,
maxvalues,
currentVelocityRatio,
localVelocityRatio,
globalVelocityRatio):
Swarm.__init__ (self,
swarmsize,
minvalues,
maxvalues,
currentVelocityRatio,
localVelocityRatio,
globalVelocityRatio)
def _finalFunc (self, position):
penalty = self._getPenalty (position, 10000.0)
finalfunc = sum (position * position)
return finalfunc + penalty
В этом коде используется метод _getPenalty(), который возвращает штраф, если значение текущих координат частицы (параметр position) выходит за пределы области определения функции (как этот предел задается, будет показано ниже). Второй коэффициент (в этом примере 10000.0) определяет, насколько жестким должен быть штраф. Метод _getPenalty() для вычисления штрафа выглядит следующим образом:
"""
Рассчитать штрафную функцию
position - координаты, для которых рассчитывается штраф
ratio - вес штрафа
"""
penalty1 = sum ([ratio * abs (coord - minval)
for coord, minval in zip (position, self.minvalues)
if coord < minval ] )
penalty2 = sum ([ratio * abs (coord - maxval)
for coord, maxval in zip (position, self.maxvalues)
if coord > maxval ] )
return penalty1 + penalty2
При желании вы можете не использовать метод _getPenalty(), а вычислять штраф непосредственно в _finalFunc() по другой формуле (например, с использованием экспоненциального нарастания штрафа вместо линейного).
Сам запуск алгоритма может выглядеть следующим образом (файл runoptimize_x2.py):
# -*- coding: UTF-8 -*-
import numpy
from swarm_x2 import Swarm_X2
from utils import printResult
if __name__ == "__main__":
iterCount = 300
dimension = 5
swarmsize = 200
minvalues = numpy.array ([-100] * dimension)
maxvalues = numpy.array ([100] * dimension)
currentVelocityRatio = 0.1
localVelocityRatio = 1.0
globalVelocityRatio = 5.0
swarm = Swarm_X2 (swarmsize,
minvalues,
maxvalues,
currentVelocityRatio,
localVelocityRatio,
globalVelocityRatio
)
for n in range (iterCount):
print "Position", swarm[0].position
print "Velocity", swarm[0].velocity
print printResult (swarm, n)
swarm.nextIteration()
Здесь мы импортируем наш класс Swarm_X2, где описана целевая фукнция, и из модуля utils импортируем функцию printResult, которая просто оформляет текущее состояние алгоритма и возвращает результат в виде строки, которую мы затем выводим в консоль.
Для простоты здесь не используются какие-либо сложные критерии останова функции, а просто алгоритм останавливается на 300-й итерации (переменная iterCount).
Наша функция будет 5-мерная (переменная dimension), то есть в формуле выше n = 5. Количество особей в рое - 200 (переменная swarmsize).
Затем мы опеределяем интервал, где мы будем искать минимум. Для этого мы заполняем массив с минимальными значениями по каждой координате 5-мерного пространства (переменная minvalues) и с максимальными (переменная maxvalues). В данном случае для всех 5 координат интервал будет [-100, 100], но в общем случае для каждой координаты могут быть свои пределы.
После задаем коэффициенты, о которых говорилось выше (переменные currentVelocityRatio, localVelocityRatio и globalVelocityRatio).
После этого в цикле 300 раз вызываем метод swarm.nextIteration(), на каждой итерации выводя текущее состояние роя и, просто из люботытства, положение и скорость одной из частицы (с номером 0, но она никак не выделяется по сравнению с другими частицами).
Чтобы получить лучшее на данной итерации решение, нужно воспользоваться свойством globalBestPosition, который возвращает список (в нашем случае с 5 элементами) со всеми координатами точки, которая в данный момент считается лучшей.
Для того, чтобы узнать значение целевой функции в лучшей на данный момент точке, в классе Swarm предусмотрено свойство globalBestFinalFunc.
Кроме того, чтобы получить одну частицу (экземпляр класса Particle), можно воспользоваться оператором индексации (как в примере, где выводятся координаты и скорость частицы).
Итак, с использованием пакета particleswarm разобрались. Теперь давайте заглянем "под капот", чтобы понять, как он работает.
Инициализация класса Swarm довольно простая, конструктор просто сохраняет переданные параметры, а затем создает нужное количество частиц со случайными значениями координат и скоростей.
"""
Базовый класс для роя частиц. Его надо переопределять для конкретной целевой функции
"""
__metaclass__ = ABCMeta
def __init__ (self,
swarmsize,
minvalues,
maxvalues,
currentVelocityRatio,
localVelocityRatio,
globalVelocityRatio):
"""
swarmsize - размер роя (количество частиц)
minvalues - список, задающий минимальные значения для каждой координаты частицы
maxvalues - список, задающий максимальные значения для каждой координаты частицы
currentVelocityRatio - общий масштабирующий коэффициент для скорости
localVelocityRatio - коэффициент, задающий влияние лучшей точки,
найденной частицей на будущую скорость
globalVelocityRatio - коэффициент, задающий влияние лучшей точки,
найденной всеми частицами на будущую скорость
"""
self.__swarmsize = swarmsize
assert len (minvalues) == len (maxvalues)
assert (localVelocityRatio + globalVelocityRatio) > 4
self.__minvalues = numpy.array (minvalues[:])
self.__maxvalues = numpy.array (maxvalues[:])
self.__currentVelocityRatio = currentVelocityRatio
self.__localVelocityRatio = localVelocityRatio
self.__globalVelocityRatio = globalVelocityRatio
self.__globalBestFinalFunc = None
self.__globalBestPosition = None
self.__swarm = self.__createSwarm ()
def __createSwarm (self):
"""
Создать рой из частиц со случайными координатами и скоростями
"""
return [Particle (self) for _ in range (self.__swarmsize) ]
На каждой итерации мы вызываем метод nextIteration(), который просто вызывает соответствующий метод у каждой из частицы в рое:
"""
Выполнить следующую итерацию алгоритма
"""
for particle in self.__swarm:
particle.nextIteration (self)
Теперь настала очередь рассмотреть класс Particle, начнем с конструктора.
"""
Класс, описывающий одну частицу
"""
def __init__ (self, swarm):
"""
swarm - экземпляр класса Swarm, хранящий параметры алгоритма,
список частиц и лучшее значение роя в целом
position - начальное положение частицы (список)
"""
# Текущее положение частицы
self.__currentPosition = self.__getInitPosition (swarm)
# Лучшее положение частицы
self.__localBestPosition = self.__currentPosition[:]
# Лучшее значение целевой функции
self.__localBestFinalFunc = swarm.getFinalFunc (self.__currentPosition)
self.__velocity = self.__getInitVelocity (swarm)
def __getInitPosition (self, swarm):
"""
Возвращает список со случайными координатами для заданного интервала изменений
"""
return numpy.random.rand (swarm.dimension) * (swarm.maxvalues - swarm.minvalues) + swarm.minvalues
def __getInitVelocity (self, swarm):
"""
Сгенерировать начальную случайную скорость
"""
assert len (swarm.minvalues) == len (self.__currentPosition)
assert len (swarm.maxvalues) == len (self.__currentPosition)
minval = -(swarm.maxvalues - swarm.minvalues)
maxval = (swarm.maxvalues - swarm.minvalues)
return numpy.random.rand (swarm.dimension) * (maxval - minval) + minval
Здесь используется функция numpy.random.rand(), которая возвращает массив заданного размера из случайных величин в интервале (0, 1).
Как вы уже можете догадаться из комментариев выше, конструктор класса Particle создает частицу со случайным начальным положением (self.__currentPosition), а также со случайной начальной скоростью (self.__velocity). Так как частица только создается, то ее начальное положение принимается за лучшее за всю историю похождения частицы (переменная self.__localBestPosition), и также сохраняется лучшее за всю историю частицы значение целевой функции (переменная self.__localBestFinalFunc)
Целевая функция у нас тоже хранится в классе Swarm (точнее, в производном от него классе), поэтому для ее расчета вызывается метод getFinalFunc() класса Swarm. Обратите внимание, что это не тот метод, который был переопределен в производном от Swarm классе. Дело в том, что метод getFinalFunc() (публичный, в отличие от переопределенного _finalFunc) не только рассчитывает значение целевой функции в переденной точке, но и смотрит, не стала ли эта точно глобально лучшей.
assert len (position) == len (self.minvalues)
finalFunc = self._finalFunc (position)
if (self.__globalBestFinalFunc == None or
finalFunc < self.__globalBestFinalFunc):
self.__globalBestFinalFunc = finalFunc
self.__globalBestPosition = position[:]
Именно внутри getFinalFunc() и вызывается наша переопределенная фукнция.
Создание частиц мы рассмотрели, вернемся теперь к методу nextIteration() класса Particle. Именно здесь содержится суть алгоритма роя частиц.
def nextIteration (self, swarm):
# Случайный вектор для коррекции скорости с учетом лучшей позиции данной частицы
rnd_currentBestPosition = numpy.random.rand (swarm.dimension)
# Случайный вектор для коррекции скорости с учетом лучшей глобальной позиции всех частиц
rnd_globalBestPosition = numpy.random.rand (swarm.dimension)
veloRatio = swarm.localVelocityRatio + swarm.globalVelocityRatio
commonRatio = (2.0 * swarm.currentVelocityRatio /
(numpy.abs (2.0 - veloRatio - numpy.sqrt (veloRatio ** 2 - 4.0 * veloRatio) ) ) )
# Посчитать новую скорость
newVelocity_part1 = commonRatio * self.__velocity
newVelocity_part2 = (commonRatio *
swarm.localVelocityRatio *
rnd_currentBestPosition *
(self.__localBestPosition - self.__currentPosition) )
newVelocity_part3 = (commonRatio *
swarm.globalVelocityRatio *
rnd_globalBestPosition *
(swarm.globalBestPosition - self.__currentPosition) )
self.__velocity = newVelocity_part1 + newVelocity_part2 + newVelocity_part3
# Обновить позицию частицы
self.__currentPosition += self.__velocity
finalFunc = swarm.getFinalFunc (self.__currentPosition)
if finalFunc < self.__localBestFinalFunc:
self.__localBestPosition = self.__currentPosition[:]
self.__localBestFinalFunc = finalFunc
Здесь реализована формула для коррекции скорости (напомню, что используется канонический вариант алгоритма с нормировкой коэффициентов), корректируется положение частицы, а затем проверяется, не стала ли новая координата лучшей для данной частицы.
Вот мы и рассмотрели реализацию алгоритма роя частиц на языке Python.
Примеры минимизируемых функций
Для демонстрации работы алгоритма в архиве с исходниками прилагаются три консольные программы для минимизации трех функций, которые обычно используются для тестирования подобных алгоритмов.
Функция сферы
Первую минимизируемую функцию мы уже видели - это фукнция
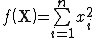
Ее глобальный (и единственный) минимум расположен в точке xi = 0, где i = 1, 2, ..., n. Значение функции в этой точке равно 0.
Ее трехмерный вид и линии уровня для n = 2 показаны ниже:
 | 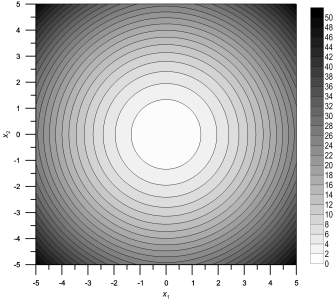 |
И пример той же функции для n = 1.
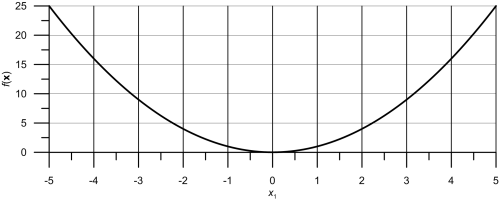
Файл в исходниках - runoptimize_x2.py
Функция Растригина
Эта функция уже посложнее, и записывается она следующим образом:
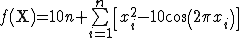
Ее трехмерный вид и линии уровня для n = 2 показаны ниже:
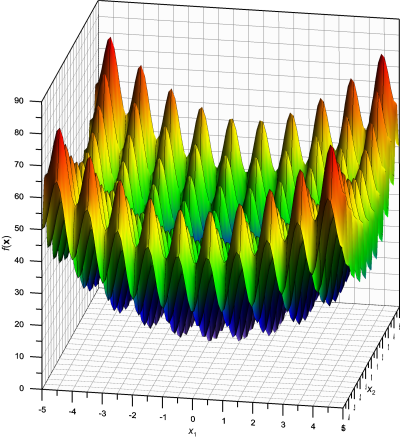 | 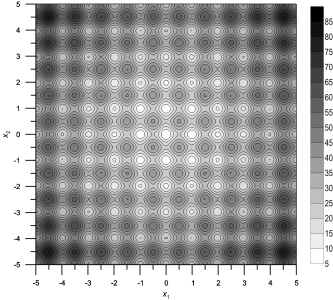 |
Функция Растригина для n = 1.

Минимум у этой функции на интервале 5.12 <= xi <= 5.12 также расположен в точке xi = 0, где i = 1, 2, ..., n. Значение функции в этой точке равно 0.
Файл в исходниках - swarm_rastrigin.py
Функция Швефеля
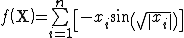
Ее трехмерный вид и линии уровня для n = 2 показаны ниже:
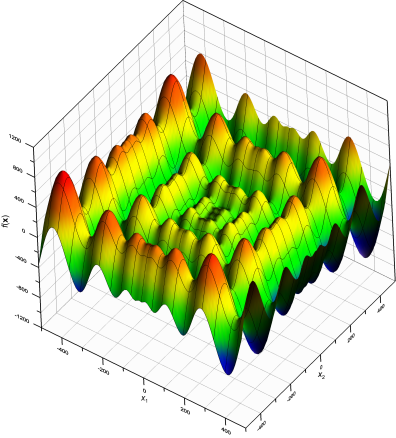 | 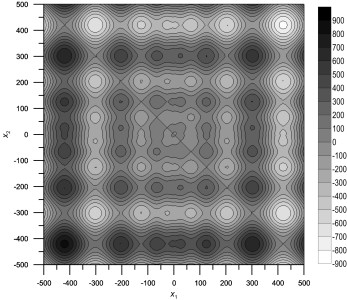 |
Функция Швефеля для n = 1.
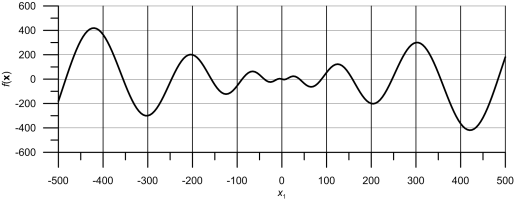
Минимум функции Швефеля на интервале -500 <= xi <= 500 расположен в точке, где xi = 420.9687 для i = 1, 2, ..., n, а значение функции в этой точке составляет f(x) = -418.9829n.
Файл в исходниках - swarm_schwefel.py.
Реализация алгоритма роя частиц на C#
В архиве с исходными текстами solution с реализацией алгоритма на C# расположен в папке .net. В отличие от реализации на Python, здесь была создана программа для наглядного представления работы алгоритма (проект ParticleGui). Программа писалась в Visual Studio 2005 под .NET 2.0, но без проблем работает под Mono и .NET 4.0.
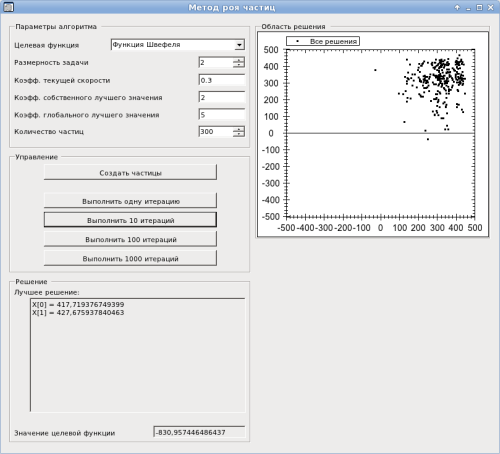
С помощью программы ParticleGui можно поиграть с коэффициентами алгоритма для различных функций и шаг за шагом пронаблюдать, как сходится (или сваливается в локальный минимум) алгоритм. Так как функция может быть многомерной, а отображать частицы нужно на двумерной картинке, то поэтому точки на картинке соответствуют первым двум координатам. Кстати, для визуализации частиц использовался компонент ZedGraph. Для примера ниже приведены первые 30 итераций для нахождения минимума функции Швефеля в виде анимации:
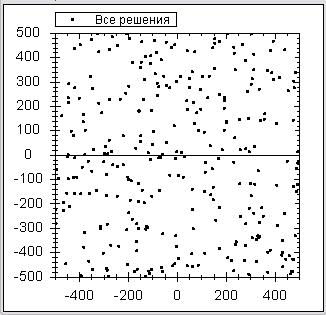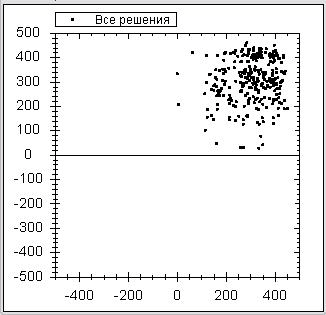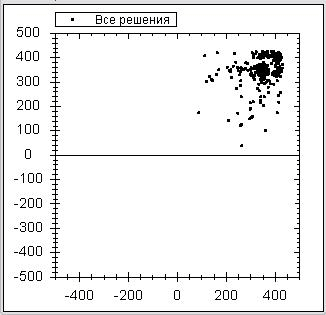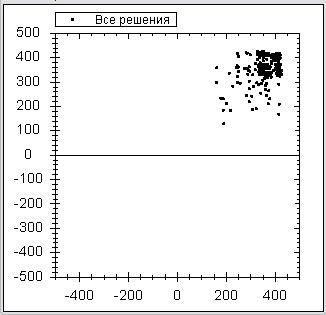
Так же подробно рассматривать реализацию алгоритма роя частиц на C#, как и на Python, мы не будем, структуры программ очень похожи. Главное отличие заключается в том, что в реализации на C# был выделен отдельный класс Task, который хранит минимизируемую функцию. Этот же класс хранит интервалы возможных изменений координат.
Структура классов показана на следующей диаграмме:
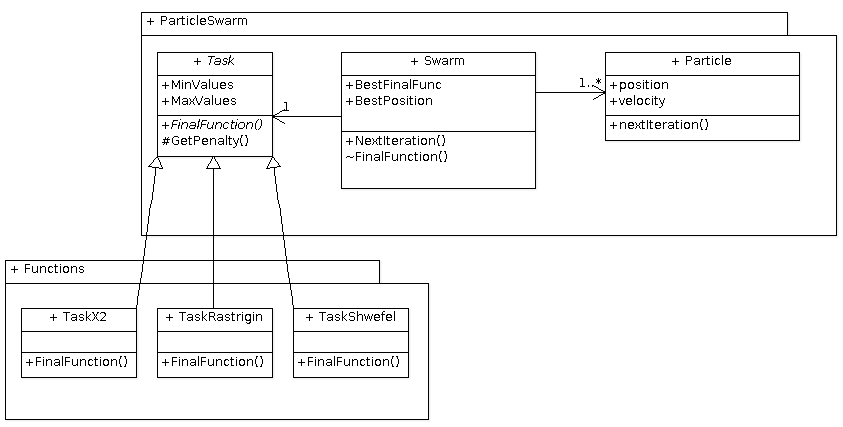
Чтобы лучше понять, как устроен алгоритм, в solution включены три консольные программы для минимизации функции сферы (проект Particle_X2_console), функции Растригина (проект Particle_Rastrigin_console) и фукнции Швефеля (проект Particle_Schwefel_console).
В качестве примера приведу исходный текст программы, минимизирующую функцию Растригина:
using ParticleSwarm;
using Functions;
namespace Particle_Rastrigin_console
{
class Program
{
static void Main (string[] args)
{
int itercount = 1000;
int dimension = 4;
int swarmsize = 3000;
double currentVelocityRatio = 0.3;
double localVelocityRatio = 2;
double globalVelocityRatio = 5;
double[] minvalues = new double[dimension];
double[] maxvalues = new double[dimension];
for (int i = 0; i < dimension; i++)
{
minvalues[i] = -5.12;
maxvalues[i] = 5.12;
}
Task task = new TaskRastrigin (minvalues, maxvalues);
Swarm swarm = new Swarm (task,
swarmsize,
currentVelocityRatio,
localVelocityRatio,
globalVelocityRatio
);
for (int iteration = 0; iteration < itercount; iteration++)
{
Console.WriteLine (Utilites.ResultToString (swarm));
swarm.NextIteration ();
}
Console.Read ();
}
}
}
Заключение
Это все, что я хотел рассказать про алгоритм роя частиц, надеюсь, что это кому-то окажется полезным. А теперь жду комментариев и оценок. :)
Вы можете подписаться на новости сайта через RSS, Группу Вконтакте или Канал в Telegram.
