Параллельно с другими проектами я продолжаю заниматься библиотекой optlib, предназначенной для оптимизации функций на языке Rust. Напомню, что под оптимизацией функции f(x) понимается нахождение такого значения x’ (в общем случае x — вектор), что значение функции f(x’) минимально на заданном интервале для x. Библиотека optlib содержит в себе алгоритмы, предназначенные для глобальной оптимизации, то есть, в отличие от градиентных методов, эти алгоритмы пытаются найти глобальный экстремум функции (градиентные методы находят только ближайший к начальной точке локальный экстремум).

До сих пор в optlib был реализован только генетический алгоритм поиска экстремума, о чем я подробно писал в статье Библиотека Optlib. Реализация генетического алгоритма оптимизации на Rust (в будущем эту статью я собираюсь переписать, потому что она теперь устарела). В новой версии библиотеки optlib был добавлен алгоритм роя частиц, о котором я когда-то писал статью Алгоритм роя частиц. Описание и реализации на языках Python и C#.

Во многом была переработана структура типов библиотеки optlib. Некоторые типажи были вынесены из модуля генетического алгоритма в общий модуль библиотеки, и теперь используются как генетическим алгоритмом, так и алгоритмом роя частиц. После публикации статьи о предыдущей версии библиотеки на Хабре, я получил много сообщений с рекомендациями того, как более правильно оформлять код в соответствии с тем, как это принято в Rust. Большинство из рекомендаций я принял к сведению и поправил код.

Кроме того, теперь от крейта optlib отпочковался новый крейт optlib-testfunc, который включает в себя различные функции для тестирования алгоритмов оптимизации. На данный момент optlib-testfunc содержит следующие функции:

• Параболоид, который описывается следующей формулой 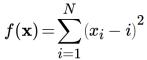 и имеет единственный экстремум в точке x’ = (1, 2, 3, …, N).
• Функция Швефеля (Schwefel function) 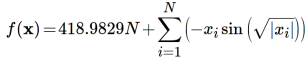. Имеет единственный глобальный экстремум в точке x’ = (420.9687, 420.9687, …). Для N = 2 график функции Швефеля выглядит так:

• Функция Растригина (Rastrigin function) 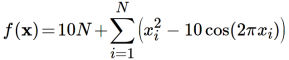. Имеет единственный глобальный экстремум в точке x’ = (0, 0, 0, …). Для N = 2 график функции Растригина выглядит так:

• Функция Розенброка (Rosenbrock function) 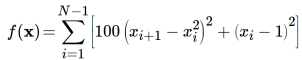. Имеет единственный глобальный экстремум в точке x’ = (1, 1, 1, …). Для N = 2 график функции Розенброка выглядит так:

В исходниках библиотеки optlib вы можете найти примеры использования генетического алгоритма и алгоритма роя частиц для оптимизации перечисленных функций. Для запуска примера в корне папки исходников введите команду

cargo run --example имя_примера --release

Где имя_примера выберите из списка:

• genetic-paraboloid
• genetic-rastrigin
• genetic-rosenbrock
• genetic-schwefel
• particleswarm-paraboloid
• particleswarm-rastrigin
• particleswarm-rosenbrock
• particleswarm-schwefel

Вот, например, как выглядит запуск примера оптимизации 15-мерной функции Швефеля:

$ cargo run --example genetic-schwefel --release

Solution:
420.974975585937500
420.969146728515625
420.955078125000000
421.004760742187500
420.999511718750000
421.007263183593750
420.987487792968750
421.001800537109375
420.980499267578125
420.991180419921875
421.001068115234375
420.942718505859375
420.964080810546875
420.951721191406250
420.961029052734375

Goal: 0.000488281250000
Iterations count: 3000
Time elapsed: 2352 ms

В будущих версиях с собираюсь добавить в библиотеку другие алгоритмы оптимизации, а также другие тестовые функции.
Ссылки:

• Optlib на github
• Optlib на crates.io
• Документация по optlib
• Optlib-testfunc на crates.io
• Документация для optlib-testfunc

PS. Вы можете подписаться на новости сайта через RSS, Группу Вконтакте или Канал в Telegram.